How To Find if Triangles are Congruent

Two triangles are congruent if they have:

  • exactly the same three sides and
  • exactly the same 3 angles.

But we don't have to know all three sides and all iii angles ...usually three out of the six is enough.

There are five ways to observe if two triangles are congruent: SSS, SAS, ASA, AAS and HL.

i. SSS (side, side, side)

SSS Triangle

SSS stands for "side, side, side" and means that we have two triangles with all 3 sides equal.

For example:

(Meet Solving SSS Triangles to find out more)

If three sides of one triangle are equal to iii sides of some other triangle, the triangles are congruent.

2. SAS (side, angle, side)

SAS Triangle

SAS stands for "side, angle, side" and means that we accept two triangles where we know two sides and the included angle are equal.

For example:

(Come across Solving SAS Triangles to detect out more)

If two sides and the included angle of one triangle are equal to the corresponding sides and bending of some other triangle, the triangles are coinciding.

3. ASA (bending, side, angle)

ASA Triangle

ASA stands for "bending, side, angle" and ways that nosotros have 2 triangles where we know ii angles and the included side are equal.

For example:

(See Solving ASA Triangles to discover out more)

If 2 angles and the included side of i triangle are equal to the corresponding angles and side of another triangle, the triangles are congruent.

4. AAS (angle, bending, side)

AAS Triangle

AAS stands for "angle, bending, side" and means that we take two triangles where we know two angles and the non-included side are equal.

For example:

(See Solving AAS Triangles to find out more)

If two angles and the non-included side of one triangle are equal to the corresponding angles and side of another triangle, the triangles are congruent.

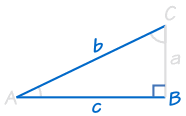
5. HL (hypotenuse, leg)

This one applies merely to right angled-triangles!

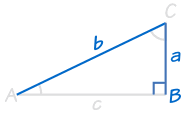triangle HL or triangle HL

HL stands for "Hypotenuse, Leg" (the longest side of a right-angled triangle is called the "hypotenuse", the other 2 sides are chosen "legs")

Information technology ways we have two correct-angled triangles with

  • the aforementioned length of hypotenuse and
  • the same length for one of the other two legs.

It doesn't matter which leg since the triangles could be rotated.

For example:

(Encounter Pythagoras' Theorem to observe out more)

If the hypotenuse and i leg of one correct-angled triangle are equal to the corresponding hypotenuse and leg of another correct-angled triangle, the two triangles are congruent.

Caution! Don't Use "AAA"

AAA means we are given all 3 angles of a triangle, simply no sides.

AAA Triangle

This is not plenty information to decide if two triangles are coinciding!

Considering the triangles tin can have the aforementioned angles but be dissimilar sizes:

Without knowing at least ane side, we can't be sure if two triangles are coinciding.